Geometrical Proportion
Like the material in arithmetical proportions, to put in a general form what Macdonald has described in his introduction “Ratios and Proportions”, an geometrical proportion is of the form ![]() . Two other ways of expressing this symbolically are a:b = c:d and a:b :: c:d. The latter symbols may be read as a is to b as c is to d. As in arithmetical proportions, the terms a and c are called antecedents and the terms b and d are called consequents. Likewise, the terms a and d are called the extremes and the terms b and c are called the means.
. Two other ways of expressing this symbolically are a:b = c:d and a:b :: c:d. The latter symbols may be read as a is to b as c is to d. As in arithmetical proportions, the terms a and c are called antecedents and the terms b and d are called consequents. Likewise, the terms a and d are called the extremes and the terms b and c are called the means.
Macdonald provides four rules for geometrical proportions. Once again, he illustrates the rules with numbers; I will do it with symbols.
- Multiplying each geometrical ratio by a constant maintains a geometrical proportion (for any constant k,
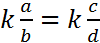 ).
). - The product of the means is equal to the product of the extremes (a x d = b x c).
- In Macdonald’s words, “If the terms of two geometrical proportions be multiplied together, term by term, that is, antecedent [by antecedent] and consequent by consequent will constitute a new proportion.” What appears in the square brackets [ ] is missing from the text in the notebook which makes it a little confusing until a numerical example is given. From Macdonald’s example, the rule is: multiply the appropriate terms in the geometrical proportion
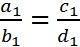 by the appropriate terms in
by the appropriate terms in 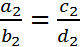 to obtain the geometrical proportion
to obtain the geometrical proportion 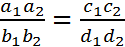 .
. - Given three of the numbers in a geometrical proportion the fourth can be determined, in Macdonald’s words, by multiplying the given means together and dividing by the given extreme (if a:b :: c:x or a:b = c:x then
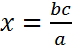 ).
).
As in arithmetical progressions, Macdonald introduces the idea of a geometrical progression which is treated later in the notebook. For a geometrical proportion in which the consequent in the first ratio is the same as the antecedent in the second ratio, the geometrical proportion ![]() is obtained. The term b is called the geometrical mean. When there is a series of continued geometrical proportions (
is obtained. The term b is called the geometrical mean. When there is a series of continued geometrical proportions (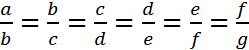 ) the distinct terms in the geometrical ratios form a geometrical progression (a, b, c, d, e, f, g are in geometrical progression).
) the distinct terms in the geometrical ratios form a geometrical progression (a, b, c, d, e, f, g are in geometrical progression).


