Sir John A Macdonald's Math Notebook
Contact Information
Email: drbell@uwo.ca
Arithmetical Progression
A series of numbers is in arithmetical progression if each number in the series is a constant increase or decrease over its preceding number. Put another way, if we take any number in the series and the number that follows it in the series and find the difference, the series is an arithmetical progression if the differences are constant. For example, Macdonald gives the series 2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32 and 35 where the difference between any number and the succeeding number is 3.
Of interest to Macdonald, or at least to his teacher, is to find the sum: 2+5+8+11+14+17+20+23+26+29+32+35
For the first time in the notebook, Macdonald uses algebra. He, or his teacher, expresses this foray into algebra quite quaintly:
“It will be of the greatest advantage in the extension of arithmetic to apply the use of letters to denote certain quantities until they are determined, that we may express our ideas clearly, fully and briefly by applying to them the signs of arithmetic.”
The letters Macdonald uses are:
a = first termd = difference between succeeding terms
n = number of terms
S = sum of the terms
In general
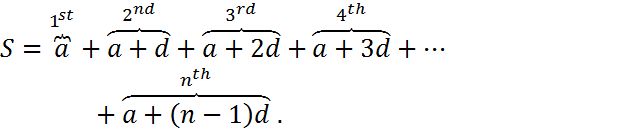
In the numerical example, a=2, d=3, n=12 and S=222.
The usual way to obtain a compact form of the sum is first to write the sum in reverse order
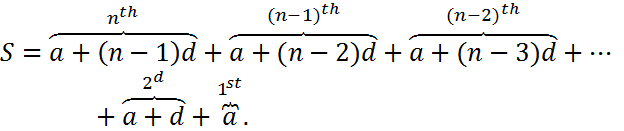
Summing the two together yields
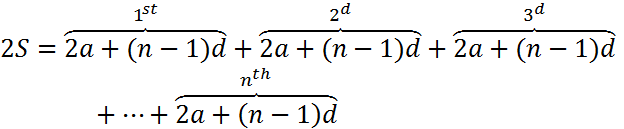
so that
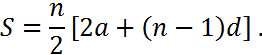
This is not quite the route that Macdonald took. His derivation is slightly different. First he assumes that is an even number. Then he adds the 1st term and the nth term, the 2nd term and the(n-1)th term, the 3rd term and the (n-2)th term, and so on. In each case the sum is 2a+(n-1)d, a constant. Since there are n/2 pairs of terms then the formula for S is obtained.
When n is odd, Macdonald explains how to find the sum by using a specific numerical example, and then says the method can be generalized to get the same formula for S. Essentially, when n is odd there are (n-1)/2 pairs (1st and nth, 2nd term and (n-1)th, and so on) that sum to 2a+(n-1)d. This leaves the middle term which is the average of the first and last terms, or [2a+(n-1)d]/2. Adding them all together yields
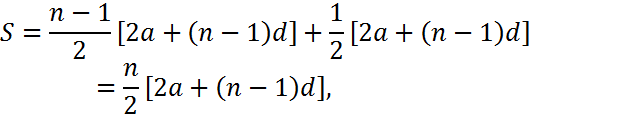
the same formula as before.
In the sum ![]() there are four terms (S, a, d, and n). Macdonald addresses the problem of given values for any three of these terms, solve for the fourth. With one exception the solution is achieved by a straightforward manipulation of the terms in the equation for S. The exception is the solution for n given S, a and d, which is the solution to a quadratic equation. In this case the equation can be written as
there are four terms (S, a, d, and n). Macdonald addresses the problem of given values for any three of these terms, solve for the fourth. With one exception the solution is achieved by a straightforward manipulation of the terms in the equation for S. The exception is the solution for n given S, a and d, which is the solution to a quadratic equation. In this case the equation can be written as
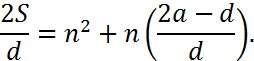
To solve for n Macdonald completes the square and obtains the equation
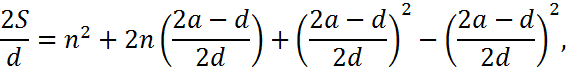
which can be rearranged to obtain
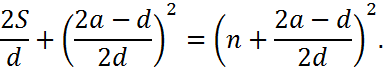
This yields
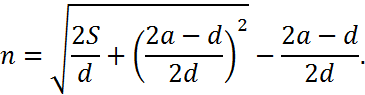
The consideration of this particular topic is odd in that Macdonald does not cover the concept of square roots until later in the notebook. When he does cover square roots, arithmetical progressions are not used in any numerical examples.


