Geometrical Progression
A series of numbers is in geometrical progression if each number in the series is a constant multiple of its preceding number. As an example, Macdonald gives the series 2, 8, 32, 128, 512, 2048, 8192, etc. so that the constant multiple is 4. The notes jump immediately into finding the sum of series in geometrical progression. When the general form of the sum is given by
where is the first term in the series, r is the ratio between succeeding terms, n is the number of terms in the sum and S is value of the sum. Macdonald derives the value for S in the usual way. Multiply both sides of the equation by r, find the difference 
, and solve for S to get 
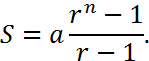
In the initial numerical example, a = 2, r = 4, and n is not given. Up to the “etc.” in the series, n = 7 in which case S = 10922.
In arithmetic textbooks and cyphering books of this era, the usual application of geometrical progressions is to the valuation of annuities at compound interest. If interest is paid at a rate of per annum, then capital of 1 invested at the rate i per annum will accumulate to 1 + i at the end of one year and 
at the end of two years (interest is earned on interest). By the same concept a value of 1 payable at the end of one year is worth 
now and a value of payable at the end of two years is worth now. This can be generalized to the value of an annuity that pays at the end of every year for years. It is worth in today’s money
which is a geometrical progression with 
and 
. Macdonald does not treat interest and annuities. In fact, no form of commercial arithmetic appears in the notebook. The whole notebook is an academic exercise rather than training to become adept at commercial arithmetic.
The three examples that Macdonald does treat are given as word problems. They all originate in Nicholas Pike’s A New and Complete System of Arithmetick. George Baxter picked, and slightly edited, the more interestingly worded examples among the ones that were available. The first two problems are to find the sum of the series; the third problem is to find the last term in the series.
- A gentleman, whose daughter was married on New Year’s day, gave her a guinea, promising to triple his gift on the first day of the month in the year. What is the ladies [sic] fortune?
Answer:
- An ignorant fop wanting to buy an elegant house, a wily gentleman told him he had one which he would sell on these moderate terms, viz. that he should give him a cent for the first door, 2 for the 2d, 4 for the 3d so on doubling at every door of which were 36 in all. It’s a bargain cries the simpleton. What did the house cost him?
Answer: $
- A merchant wanting to buy a cargo of horses for the West Indies, a jockey told him he would take all the trouble and expense on himself of collecting 30 horses for [the] voyage if he would give him the value of the last horse at the rate of ½ for the first, 2d for the 2d, 4d for the 3d so on. What was the value of the last horse? [The problem and solution are stated in pounds, shillings and pence. One penny is abbreviated 1d and one shilling is 1s. Under the pre-decimal system in the United Kingdom £1 = 20s and 1s = 12d, i.e. 20 shillings to the pound and 12 pence to the shilling. With the problem stated in pence, Macdonald expressed his answer in pounds, shillings, and pence.]
Answer: £ s d
