Application and Use of the Square Root
Macdonald lists seven problems all requiring the calculation of a square root in the solution. For the most part, each problem is described generally, and then a general rule is given to solve it. In each case at least one numerical example is given to illustrate the problem and the rule. The first six problems are numbered. In this group, some of these problems involve the concept of geometrical proportion. Others involve the area of a circle or the area of an ellipse. The rules are given such that the student did not need to know the formula, for example, for the area of a circle. The problems are set to provide the student practice in calculation not in understanding the geometrical concepts and relations. All the problems in this part of the notebook are taken from Nicholas Pike’s A New and Complete System of Arithmetick, pp. 171 – 175.
Problem 1st
Required: the mean proportional between 24 and 96.
Solution: This is the geometric mean covered in geometrical proportions. The solution is ![]() .
.
Problem 2d
To find the side of a square equal in area in any given superficies whatever.
Initially, the statement of the problem is vague. Without reading the notebook further, the first thing I did was to look up in the Oxford English Dictionary what “superficies” means. It turns out to be, with respect to geometry, “a continuous extent having only two dimensions (length and breadth, without thickness).” The question becomes perfectly clear when Macdonald finally turns his problem into a numerical one. Later under this problem he writes, “If the area of a circle be ![]() what is the side of a square equal in area thereto?”
what is the side of a square equal in area thereto?”
Solution:
![]() or
or ![]() to three decimal places.
to three decimal places.
Problem 3d
If it be required to place a number of men in rank and file or to plant a number of trees or other objects so that the rank may be to the file or in other words the length may be to the breadth in a given ratio and so that there may be a given distance between man and man, tree and tree, or object and object you will find how many must be placed in rank or length or in file or breadth likewise how many square feet or yards they stand upon by the following rule.
Comment: The problem is an exercise in geometrical proportions and square roots.
Rule: As the ratio in length is to the ratio in breadth so is the number of men, trees, &c to a fourth number whose square root is the number in breadth; and as the ratio in breadth is to the ratio in length so is the number of things to a fourth number whose square root is the number in length. As unity is to the distance so is the number in length to a fourth number; as unit [is] to the distance so it the number in breadth to a fourth number. These two numbers last found multiplied together will give the square feet or yards upon which they stand.
Example: I would set out and orchard of 600 trees so that the length shall be to the breadth as 3 to 2 and the distance of each tree from the other 7 yards. How many trees must there be in length? And how many square yards do they stand upon?
Solution
Here is Macdonald’s solution with a bit more detail. Let , , and be the unknown fourth numbers
3:2 :: 600:w or w=400 so that ![]() is the length
is the length
2:3 :: 400:x or x=900 so that ![]() is the breadth
is the breadth
What is not explicitly stated is that since is the number of trees in length then is the number of units of distance in length. Likewise is the number of units of distance in breadth.
Therefore,
1:7 :: 19:y so that y:19x7=133 and 1:7 ::29:z so that z=29x7=203.
Consequently, the whole plot is 133x203=26999 square yards. Macdonald writes the answer as 26999 square feet, again showing his lack of attention to the problem.
Problem 4th
If a leaden pipe or other conductor will fill a cistern in a given time it is required to find the diameter of another pipe which will fill the same cistern in any required time.
Comment: The problem is an exercise in geometrical proportions and square roots.
Rule: The squares of the diameters as inversely as the times.
Examples
- If a leaden pipe of an inch in diameter will fill a cistern in 3 hours I want to find the diameter of another pipe which will fill the same cistern in 1 hour.
Solution: 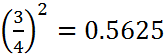 . Let x be the desired number (the square of the desired diameter). Since the time varies inversely with the diameter, then we have the geometrical proportion
. Let x be the desired number (the square of the desired diameter). Since the time varies inversely with the diameter, then we have the geometrical proportion ![]() or
or ![]() or
or ![]() , which yields
, which yields ![]() . The desired diameter is
. The desired diameter is ![]() to three decimal places.
to three decimal places.
Comment: Macdonald did not pay close attention to what he was copying. He wrote the solution in the form 1:0.5625 :: -1.29 without any intermediate steps. The statement as given appears odd. If he meant instead of (which he probably did not) the statement is incorrect. He was probably just hurrying to write down the answer, which is not quite correct as he has given it.
- If a pipe whose diameter is
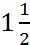 inches will fill a cistern in 5 hours at what time will a pipe whose diameter is
inches will fill a cistern in 5 hours at what time will a pipe whose diameter is 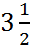 inches fill the same cistern.
inches fill the same cistern.
Solution: 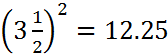 and
and 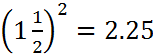 . Let x be the desired time. Then x:2.25 :: 5:12.25 or x=0.9183673 hours. Macdonald expresses his answer in minutes so that the answer in minutes is 55.1.
. Let x be the desired time. Then x:2.25 :: 5:12.25 or x=0.9183673 hours. Macdonald expresses his answer in minutes so that the answer in minutes is 55.1.
Comment: (1) This problem has nothing to do with finding a square root. (2) Macdonald gives 55.6 minutes as his answer because in his longhand division he incorrectly converts the hours to minutes at one point. Here is what he did.
He first found 5x2.25 to get 11.25. Then he converted to minutes by multiplying by 60 for which he correctly obtains 675. Then he divides 12.25 into 675. Macdonald’s longhand division looks like this:
|
|
55.6 |
|
1225 |
67500 |
|
|
6125 |
|
|
6250 |
|
|
6125 |
|
|
125 |
|
|
×60 |
|
|
7500 |
|
|
7350 |
|
|
150 |
Where is his error? Can you explain why he made this error?
- If a pipe 6 inches bore will take 4 hours in running a certain quantity of water in what time will 3 pipes each 3 inches bore be in discharging double the quantity?
Solution: 6x6=36 for the one pipe and 3x3=9 for one of the 3 pipes which yields 9x3=27. Without doubling, let x be the quantity of water. Therefore 27:4 :: 36:x so that ![]() . Since the quantity of water must be doubled then the solution is
. Since the quantity of water must be doubled then the solution is ![]() hours or 10 hours and 40 minutes.
hours or 10 hours and 40 minutes.
Comment: (1) Once again, this problem has nothing to do with finding a square root. (2) Macdonald answer is 6 hours. Where he erred was in the size of the set of 3 pipes. In his calculation he gives the 3 pipes a 4-inch bore rather than a 3-inch bore. This results in the relation 48:4 :: 36:x so that x=3. When the quantity of water is doubled, the time doubles to 6 hours. The 4-inch bore comes from Nicholas Pike’s A New and Complete System of Arithmetick, p. 174. Perhaps Macdonald copied the statement of the problem incorrectly.
Problem 5th
Given the diameter of one circle to make another circle which shall be any number of times greater or less than the given circle.
Rule: Square the given diameter and if the required circle be greater multiply the square of the diameter by the proportion and the root of the product will be the required diameter. But if the required circle be less, divide the square of the diameter by the proportion and the root of the quotient will be the diameter required.
Comment: No results in geometry are covered in the notebook. Given the statement of the rule no knowledge of geometry is necessary.
Example: There is a circle whose diameter is 4 inches. I want to know the diameter of a circle 3 times as big.
Solution: Square the diameter: 4x4=16. Multiply by the increase in size: 16x3=48. The solution is ![]() , which can be found longhand by the algorithm given earlier in Macdonald’s notes, which was taken from Nicholas Pike’s A New and Complete System of Arithmetick.
, which can be found longhand by the algorithm given earlier in Macdonald’s notes, which was taken from Nicholas Pike’s A New and Complete System of Arithmetick.
Problem 6th
To find the diameter of a circle equal in area to an ellipsis (or oval) whose transverse and conjugate diameters are given.
Rule: Multiply the two diameters of the ellipsis together and the square root of that product will be the diameter of the circle equal to the ellipsis.
Comment: No results in geometry are covered in the notebook including the area of a circle which ![]() is where r is the radius, or the relation between the area of a circle and the area of an ellipse. The area of the ellipse is
is where r is the radius, or the relation between the area of a circle and the area of an ellipse. The area of the ellipse is ![]() , where a is the length of the semi-major axis and b is the length of the semi-minor axis. The circle is the special case of the ellipse in which r=a=b. Given the statement of the rule no knowledge of any of this material is necessary.
, where a is the length of the semi-major axis and b is the length of the semi-minor axis. The circle is the special case of the ellipse in which r=a=b. Given the statement of the rule no knowledge of any of this material is necessary.
Example: The transverse diameter of a circle [sic] is 48 yds and the conjugate is 36. What is the diameter of an equal circle?
Comment: Once again Macdonald is not paying attention to what he is doing. The transverse diameter should be of an ellipse.
Solution: Multiply the two diameters together to get 48x36=1728. Then ![]() , which can be found longhand by the algorithm given earlier in Macdonald’s notes, which was taken from Nicholas Pike’s A New and Complete System of Arithmetick. For some unexplained reason Macdonald has +18239 tacked on to the end of his answer.
, which can be found longhand by the algorithm given earlier in Macdonald’s notes, which was taken from Nicholas Pike’s A New and Complete System of Arithmetick. For some unexplained reason Macdonald has +18239 tacked on to the end of his answer.
The final problems are applications of what is known as Pythagoras’ Theorem in geometry. Macdonald has copied in the notebook, “The following questions may be all solved by Euclid 1st Book Prop 47”. This proposition reads, “In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle.” This part of the notebook contains the only set of diagrams related to the arithmetical problems that Macdonald is solving. Here is one page from this section.



